トップ 更新履歴 プロフィール このサイ トの説明 工作部屋 3DCG Ｃ言語 プログラム RPGツ クール 自 作MIDI 自作 ＰＣ STAR WARS部屋 ノベル ラ イトセーバー 3DCG 日記 BBS リンク Creative Chamber mobile 携帯用の壁紙等を載せています。 お立ち寄りのさいは、 是非ランキングサイト等への投票をお願いします。

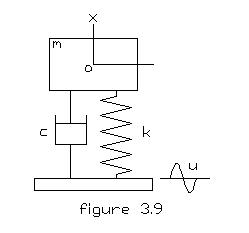
変位による強制振動 　支持台が強制周期変位をして、これにより生ずる質量mの運動をシミュレーションし、アニメーション表示をする。 シミュレーションの方法はオイラー前進解法。（簡単だし） 下準備 プログラム作成 運動の観察 　図3.9に示す支持台に強制変 位が作用する場合を考える。 　いま静つり合いにある質量mの重心を原点にとり、図3.9のようにx軸をとる。支持台に作用する上下方向の強制変位をu、これにより生ずるmの変位をx とする。このとき支持台に対するmの相対変位は x-u となり、mに作用するばね力は -k(x-u) 、粘性減衰力は -c(dx/dt - du/dt) である。 　したがってmの運動方程式は、 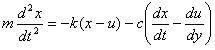          ・・・・・・・・・・(1) 　ここでmの絶対速度をvとおくと、vは、 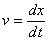          ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ (2) となる。式(2)を式(1)に代入すると、 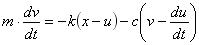         ・・・・・・・・・・・・(3) となり、式(2)、式(3)より、式(1)は一階連立常微分方程式で表すことができる。 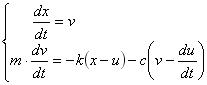          ・・・・・・・・・・・(4) 　ここで、微分の定義を考えて、式(4)を変形すると、 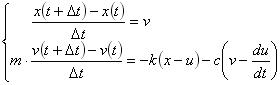          ・・(5)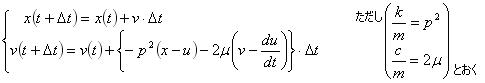           ・・・(6) 　式(6)の右辺は時刻tの状態、左辺は時刻t+Δtの状態を表している。 　いま、支持台の強制周期変位を、 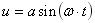          ・・・・・・・・・・・・・・・・・・・・・・・・ (7) の場合について考えると式(6)は、 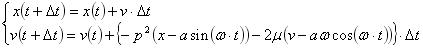          ・・・・・・・・・・(8) となる。式(8)をもとにプログラムを作成する。 　実際にコーディングするまえに、簡単な仕様を考え ておきま す。 mの座標等の変数はグローバルで宣言する。（ローカルの方がいいんだろうけど、面倒だし…） 関数void Init_State(void)をつくり、初期状態を設定する。 初期状態は、mが静つり合い状態。 関数void Input_Data(void)をつくり、減衰比、p、ωを入力させる。 関数void myInit( char *)をつくり、ウインドウやキーボードの設定なんかをやる。（たぶん） 関数void Calculate(void)をつくり、式(7),(8)をもとに、m、支持台の座標の計算を行う。 関数void draw(void)をつくり、m(Box)、支持台、バネを描く。 関数void display(void)をつくり、drawで描いた図をディスプレイに表示させる。 関数void move(void)をつくり、時刻tをDELTA_Tだけ進める。 関数void myKbd( unsigned char, int, int)をつくり、ESCキーが押されるとプログラムを強制終了、"r"又は"R"が押されると時刻tを0に戻して最初からアニメーションを始める。 m(Box)が支持台を突き抜けても気にしない。 これを元に作ったプログラムはこちら→　figure3_9.c　 ←downloadは右クリックから 　一応、プログラムがちゃんと動くか確かめます。 　方法は、動きがはっきりとする特別な条件を入力して、予想通りの動きをするかを確かめます。これから特別な条件を探していきます。 　まず、m(Box)の相対座標xrを考えます。すなわち、 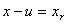          ・・・・・・・・・・・(9) とおく。これを式(1)に代入、また式(7)も代入し整理すると、 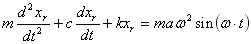          ・・・・・・・・・・(10) 式(6)と同様に k/m =p2 、 c/m =2μ とおくと、 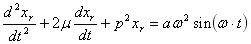          ・・・・・・・・・・・・(11) となる。 　定常強制振動を調べるため、式(11)の特解を求める。（式(11)の一般解は、補関数と特解の和で表さ れるが、補関数の方は自然振動を表しており、時間とともに消滅する。特解は定常強制振動を表す。）ここで、 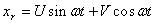                    ・・・・・・・・・・・・・・・・・・・・・・・・・・ (12) とおく。式(12)を式(11)に代入すると、 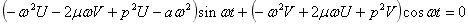          ・・・・・・・・(13) 式(13)が時刻tにかかわらず成り立つためには、sinωt、cosωtの係数が0とならなければならない。それぞれの係数=0とおいて式を整理する と、 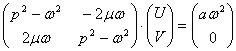          ・・・・・・・・・・・・・・(14) 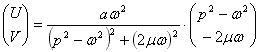          ・・・・・・・・・・・(15) 式(15)を式(12)に代入すると、式(11)の特解を求めることができる。ここで、定常強制振動応答（式(12))を、 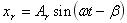          ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ (16) と変形する。振幅Arと位相差βはそれぞれ、 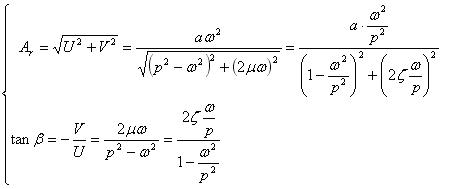          ・・・・・・・・・・(17) となる。 　ζをパラメータとしてAr/a、ω/pの関係を図示すると、図3.10が得られる。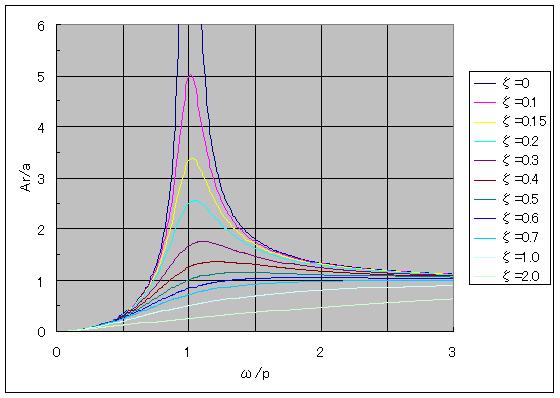                                             figure 3.10 図3.10よりω<<pのときはAｒはほとんど0すなわちx≒uとなり、mは支持台とほとんど同じ運動をする。 ζが小のときは、ωがpに近づくにつれてmの振動は増大して極大に達し共振を生ずる。その位置はδAr/δ(ω/p) =0 を満足する、 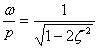          ・・・・・・・・・・・・・・(18) において起こり、そのときの振幅は式(18)を式(17)に代入して、 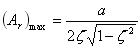          ・・・・・・・・(19) となる。ζが1/√2より大きい場合は極大値は生じない。 ω>>pにおいてはArはほとんどa、βはほとんど180°となるから、 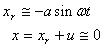          ・・・・・・・・・・・・(20) すなわちmはほとんど静止の状態にあり、支持台のみがuで動いていることとなる。 以上3つの条件を入力し、動きを観察し、動作確認をすることができる。 参考：斉藤秀雄著『工業基礎振動学』（用賢堂、2004）